昇圧チョッパー回路のスイッチング周波数の計算

DC-DCの昇圧回路としてメジャーな昇圧チョッパー回路。スイッチング周波数の計算方法がいまいちよくわからない。。。
可変抵抗を回して調節するのもアリですが、マイコン等で制御しようとするとするとそうもいきません。
はたして昇圧チョッパー回路のスイッチング周波数はいかにして求まるのでしょうか。

昇圧チョッパー回路の設計

回路の動作原理の説明は昇圧チョッパー回路の原理をご参照ください。

最適な周波数とは

そもそも、最適な周波数とは、どのような周波数なのでしょうか？
最適な周波数とは、コイル電流が適切な時に、コイル電流を遮断する、無駄のない周波数のことです。今回はこの周波数を、計算により求めてみます。
ところで、昇圧チョッパー回路の原理は、コイルにエネルギーをため、そのエネルギーを放出していると考えることもできます。
出力されるエネルギーは、コイルにためられたエネルギーから損失を引いたものです。コイルにたまったエネルギーが多きければ大きいほど、出力されるエネルギーは大きくなります。昇圧チョッパー回路はDC-DCで動作しますので、電源電圧は一定です。よってコイルためられたエネルギーの大きさはコイル電流の大きさで決まります。
さて、昇圧チョッパー回路の基本回路を以下に示します。

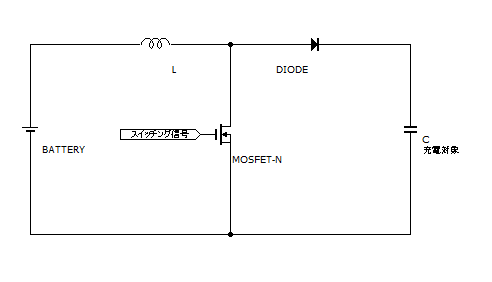
昇圧チョッパー基本回路

スイッチング素子としてFETを使用し、コンデンサに充電します。
今回求めたいのは"最適な周波数"つまり"コイル電流が適切な時に、コイル電流を遮断する、無駄のない周波数"ということになります。
FETがonになってからの経過時間をt、コイル電流をiとすると、今回求めたいのは、コイル電流がiのときの経過時間tということになります。
では、FETがONの時の場合を考え、回路の電圧方程式を立てましょう。
FETのon抵抗を考えると、FETがオンの時、回路は普通のLR直列回路と変わりありません。
時間をt、電流をi、インダクタンスをL、FETのon抵抗をR、電源電圧をEとし、t=0のときFETがONになるとします。
コイルの逆起電力をEとすると、（今回だけEを逆起電力と置おきましたが、他では電源電圧です。）
E=L(di/dt)

Rの電圧降下は電流と抵抗値の積です。よって、回路の電圧方程式は、
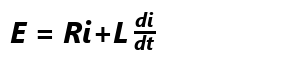
E=ri+L(di/dt)
となります。

微分方程式

さて、回路方程式がわかったところで、最適なスイッチング周波数を求めてみましょう。
経過時間をt、電流をi、インダクタンスをL、FETのon抵抗をR、電源電圧をEとします。また、初期条件は、t=0のとき、i=0です。
求めたいのは、電流がiのときの時間tでした。

FETがONの時、回路はRL直列回路となるため、キルヒホッフの法則より、回路方程式は、
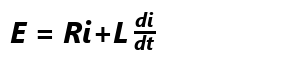
E=ri+L(di/dt)
となり、これをtについて解けば、電流がiのときの時間tを求めることができます。

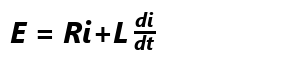E=ri+L(di/dt)両辺からRiを引いて、
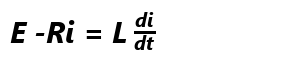E-ri=L(di/dt)両辺をLでわって、
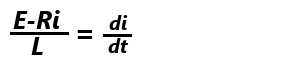L/(E-ri)=(di/dt)両辺の逆数をとり、(1/L)diをかけて、
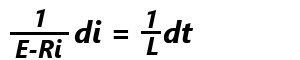{1/(E-ri)}di=(1/L)dt両辺を積分して、
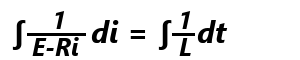∫{1/(E-ri)}di=∫(1/L)dtiの係数は-R、左辺は∫(1/x)dxの形なので、
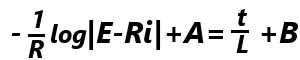-(1/r)log|E-ri|+A=(1/L)+B(A,Bは積分定数)、Ri＜Eより、E-Ri＞0よって、
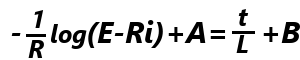-(1/r)log(E-ri)+A=(1/L)+B両辺からBを引いて、A-BをCと置き、
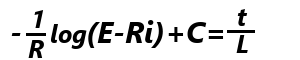-(1/r)log(E-ri)+C=(1/L)変形して、
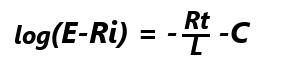log(E-ri)=-(rt/L)-C展開して、
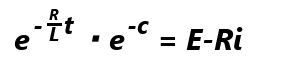e^{-(r/L)t}e^(-c)=E-riここで初期条件を代入します。t=0の時、i=0のため、
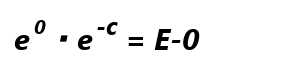e^0e^(-c)=E-0よって、
e^(-c)=Eより、
E[e^{-(r/L)t}]=E-ri両辺をEで割り、対数をとります。
log[e^{-(r/L)t}]=log{1-(r/E)i}
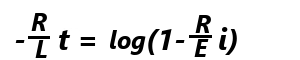-(r/L)t=log{1-(r/E)i}両辺に(-L/R)をかけて、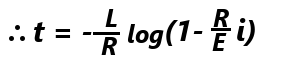
t=-(L/r)log{1-(r/E)i}

微分方程式は解けました。今回求めたtは、コイル電流がiの時の経過時間です。
d比を50%とすれば、周期は2tとなりますので、最適な周波数はその逆数、と求めることができます。
実際の計算を手でやるのは面倒なので、excel等のソフトを利用して、コンピューターに解いてもらうのが賢明でしょう。

関連記事

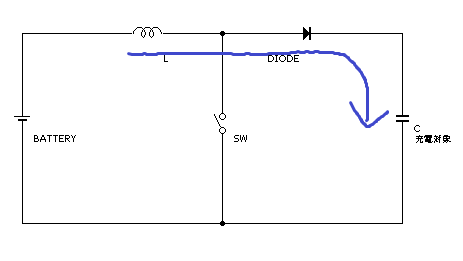昇圧チョッパー回路の原理昇圧チョッパー回路の原理
DC-DCの昇圧回路としてメジャーな昇圧チョッパー回路。しかし、昇圧チョッパー回路はなぜ"昇圧"できるのでしょうか。
初心者向けに解説し、おまけとして簡単な設計方法を紹介します。