微分の公式

接線の傾きを求める微分法。極限まで小さい分母や面倒な式変形。。。
実は微分には覚えておきたい公式が存在します。微分の計算を魔法のように簡単にしてくれる公式。ぜひとも覚えておきましょう。

微分とは

微分とは、ご存じのとおり、接線の傾きを求めることです。ご存じない方は、完全マスター微分法で基礎から詳しく解説しています。
さて、微分の計算って完全マスター微分法のようにやったら面倒じゃないですか？
しかし、安心してください。導関数には決まった規則があります。それが”微分の公式”です。

微分の公式

べき関数の微分

べき関数

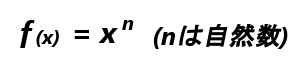
のような関数をべき関数といいます。２次関数も３次関数も１次関数も全部べき関数です。
まずは、１次関数
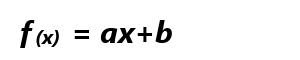
f(x)=ax+b
の導関数を求めます。
(ax+b)'=a
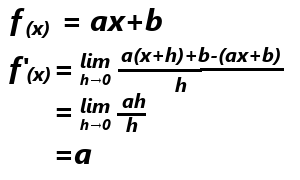
以下同様に２次関数、３次関数の導関数を求めます。※計算過程は省略
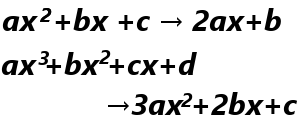
x^2,X^3'=2x,3x^2

さて、べき関数の導関数の規則性、
x^a'=ax^a-1

に気づきましたか？べき関数の導関数は、
x^a'=ax^a-1

となります。

指数関数

a^x

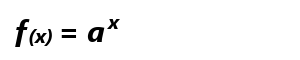
のような関数を指数関数といいます。右上のxを指数、aを底とよびます。
さて、導関数を求めてみましょう。
a^x'=a^x

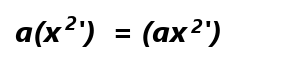
となります。指数関数は微分しても同じまんまなんですね。

係数

ここで今更ではありますが、微分では、係数を外に出して計算することができます。
要するに、

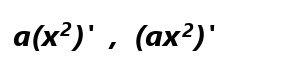
a(x^2)'=(ax^2)'
は、同じ結果を導くということです。ここではめんどくさいので証明は割愛します。

まとめ

ほかにも三角関数などの導関数も含め、一覧表にまとめてみました。ぜひご活用ください。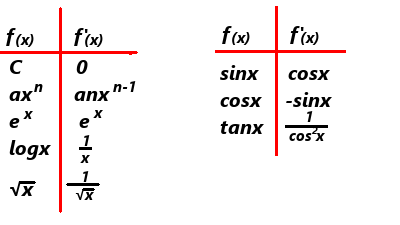

figure1

関連記事

２次関数の頂点の求め方完全マスター微分法
あらゆるところで活躍してくれる強い味方、”微分法”。でも正直難しくってわからない。。。
そんな人は意外と多い。そこで、この”完全マスター微分法”では、できるだけわかりやすく丁寧に、基礎から微分法を解説します。微分習ったけどわけわかんねーよwそんなあなたでも大丈夫。これを読めばきっと”微分”がわかるようになりますよ。