完全マスター微分法
あらゆるところで活躍してくれる強い味方、”微分法”。でも正直難しくってわからない。。。そんな人は意外と多い。そこで、この”完全マスター微分法”では、できるだけわかりやすく丁寧に、基礎から微分法を解説します。
微分習ったけどわけわかんねーよw
そんなあなたでも大丈夫。これを読めばきっと”微分”がわかるようになりますよ。
予備知識
平均変化率
微分の解説に入る前に、平均変化率について説明しておきます。平均変化率とは、中学校でいうところの”変化の割合”と同じです。
ある区間における、xの増加量に対するyの増加量を平均変化率といいます。
ある区間において、xが5増加したら、yが10増加した。この時の平均変化率は２です。
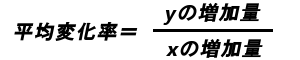
たとえば、100mを10secで走る選手Ａさんがいたとしましょう。
単純に計算すると、Ａさんは10m/sの速さで走っていることになります。しかし、実際にはAさんのある瞬間、瞬間における速度は10m/sとは限りません。スタート直後のAさんの速度は0m/sです。常に加速しつづけます。
しかし、10secの間隔でみてみると、Aさんは常に10m/sで走ったのと等しいのです。
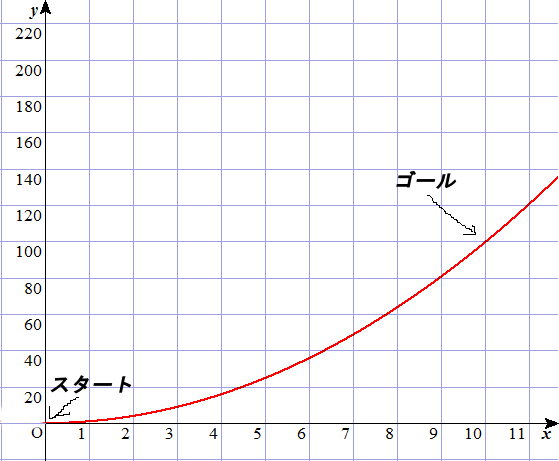
Aさんの実際の進行のようす。横軸が時間。縦軸が距離を表す。最初の２秒間で進んだ距離と、最後の２秒間で進んだ距離は同じ２秒間でも違う。
ある区間においてAさんが進んだ距離を、時間で割れば平均速度を求めることができます。
Aさんが10秒間で進んだ距離は100m、よって平均速度は10m/sとなります。
この平均速度こそが、まさしく平均変化率なのです。以下の図をご覧ください。
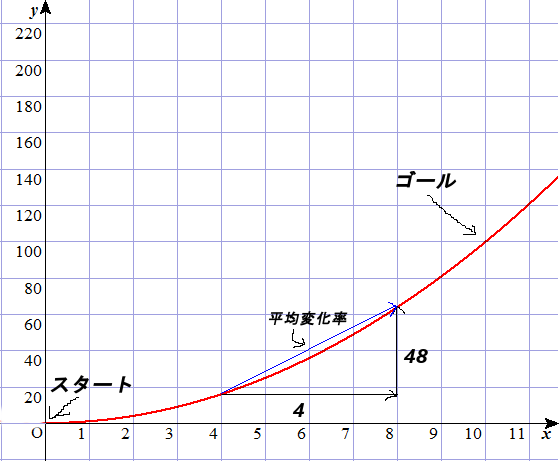
ある区間（xの領域のこと、定義域とも。上記における4から8）における、xの増加量（上の図では４）に対するyの増加量（上の図では48）が、平均変化率となります。
したがって、上図では、青矢印の傾きが平均変化率を表し、平均変化率は12です。
この平均変化率の考え方は、微分の概念において、非常に重要なので覚えておいてください。
極限
微分の概念において、もう一つ外せないのが極限の考え方です。極限とは何か。
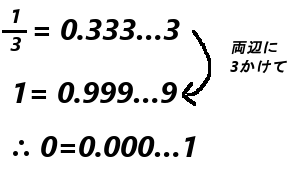
最後の式、これが極限の前提です。
数直線上に、a,bの２点を取り、bをaに極限まで近づけます。
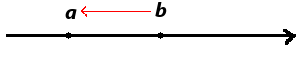
bをaに極限まで近づけただけなので、２点は異なる2点です。お互いの間には無限に小さい距離があります。
無限に小さい距離、すなわち 0.000…1 離れた2点a,b。 0.000…1=0 なのでa,b間の距離は0です。つまり２点は重なっていると”みなす”ことができるというわけです。しかし、実際、2点は異なります。
ここで、上記の”bをaに極限まで近づける”ということを、数学では記号limを用いて以下のように表します。
上以外にも、たとえば以下のような記述をすることがあります。
上記の表記は関数が区分的に連続である場合には使えますが、そうでない場合は微分の結果が異なることがあるため、以下の表記をします。
なお、極限は英語ではlimit、ラテン語ではlimesというらしいです。
微分法
さあいよいよ本題の微分の解説に移ります。微分とは
微分とは、傾きを求めることです。一次関数の傾きは常に一定ですが、二次関数や三角関数などの関数の傾きは場所によって変わります。
では曲線の傾きとは何でしょう。ズバリそれは、、、接線の傾きのことを指します。
曲線と接する直線の傾きを、接点における曲線の傾きと定義するわけです。この傾きのことを微分係数といいます。 つまり、微分とは傾きを求めることであり、微分係数を求めることでもあるのです。 さて、ではどのようにして曲線の傾きを求めることができるのでしょうか？
微分係数の求め方
まずは関数、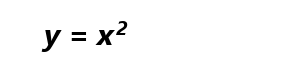
について考えます。
関数上の２点間における傾き、すなわち微分係数を求める方法は上記で説明したとおりです。
つまり、関数の２点間の傾きを求めることはできます。
では、任意の区間a,bにおける平均変化率はどうなるでしょうか。
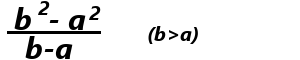
ここで、bをaに極限まで近づけ、平均変化率を求めます。お互いの間の距離は無限に小さいので、極限まで0に近い数"h"を用いて、bを(a+h)と置き換えます。
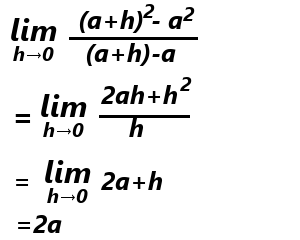
極限まで近い２点は重なっているとみなせるため、極限まで近いa,b間の傾きは、aにおける傾きと等しいわけです。
つまり！aにおける微分係数を求めることができました！
極限まで近い関数上の2点間 a,b の傾きは、aにおける傾き、つまり微分係数に等しい。これが微分法です！
平均変化率の極限をとれば、微分係数となるわけです。
これを使えば、関数、
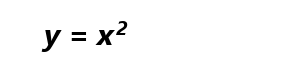
の(2,4)における傾きは4、(9,81）における傾きは18と求めることができます。
数学的にはy=f(x)の微分を以下のように表します。
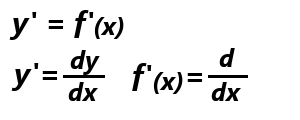
導関数
個々の定数、x=a のときの微分係数は求めることができました。ここで、xの値にその微分係数を対応させた関数を考えてみましょう。この関数を導関数とよびます。
では具体的に導関数とはどのようなものなのでしょうか。ここでは例として、
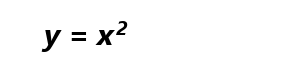
の導関数を求めてみます。
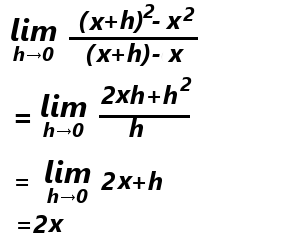
導関数とは、横軸にx、縦軸にf'(x)をとった関数ともいえます。
今までは、f'(a)=2a と、個々の定数に対して求めていた微分係数を、変数xをもちいて、f'(x)=2x と置き換えただけです。
この傾きの関数、導関数は三次関数、四次関数などの高次の関数のグラフの作図に使用したり、物理の問題で使ったりと大変重要な考え方なので、おさえておきましょう。
終わりに
これで微分法の概念と計算法を理解できたと思いますがどうでしょうか？「ここがわからない。」「ここの意味を教えて。」等のリクエストや質問がございましたら遠慮なく質問してください。
twitterでリプライやＤＭくれればできるだけわかりやすく返信します。連絡先はこちらです。
関連記事
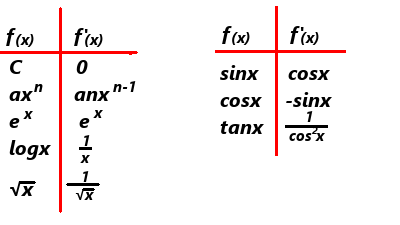微分の公式今回の完全マスター微分法のように曲線の傾きを求めるに、分数に極限が入ったような式を計算せずに一瞬で導関数を求めることができる、魔法の公式を紹介します。
微分には一定の規則性があるので、それを覚えれば大幅な時間短縮が見込めます。
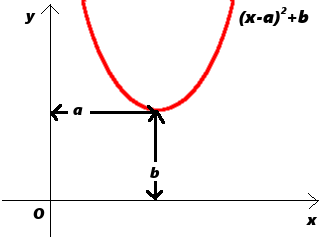二次関数の頂点の求め方今回マスターした微分法を使えば、難しい式変形して求めなければならない２次関数の頂点を、圧倒的に簡単に求めることが可能です。しかも、式変形がややこしいほど、微分法で解いた方が、速く、正確に計算が終わります。ぜひ微分法をもちいた頂点の求め方をマスターして、ライバルをあっと言わせてください！