二次関数の頂点の求め方

世の中の物理現象、実は２乗に比例するものが非常に多いんです。
物理の問題では、２次関数の頂点を求める必要にかられることがしばしば、、、
２次関数の頂点の通常の求め方と、裏技的な計算の楽な解き方を合わせて3つ紹介します。
これで君も２次関数のテストで時間が足りないなんてことはないでしょう！

平方完成

まずはみんながやってる平方完成。おそらくもっとも一般的な方法です。
簡単に言うと、強引にカッコの２乗を作ってしまう方法です。

たとえば関数、

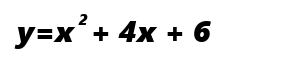
これは、

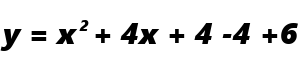
と変形できます。つまり、

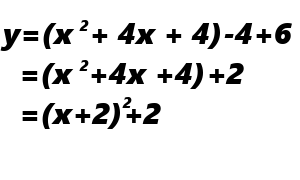
このように、カッコの２乗を作ることができます。










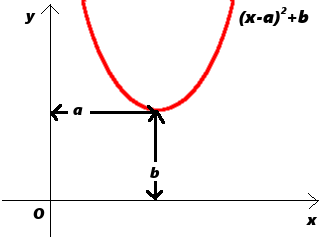
ここで、


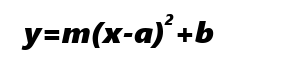
における頂点は、(a,b)となります（左図）。


よって、

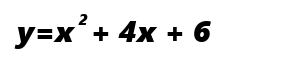
の頂点は、(-2,2)と求めることができます。
これが一般的な平方完成と呼ばれる手法で頂点を求める方法です。
カッコの２乗を作ることによって簡単に頂点を求めれるように見えます。
ただし、以下のような場合はどうでしょうか？


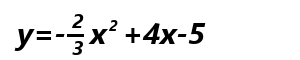
計算が非常に厄介で、計算ミスを起こす可能性が非常に高いです。
管理人はこの手の問題が出されたとき、計算ミスで15点しか取れませんでした（）
そこで思いついたのが以下の二つの解法。非常に単純で、計算も楽です。

一般化

2次関数、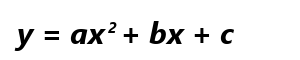


の頂点を、平方完成によって導出します。すると、、、

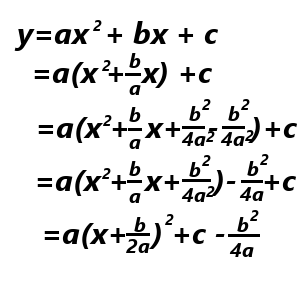
つまり、


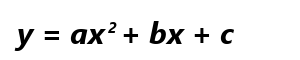
の頂点は、



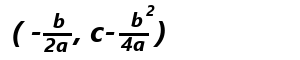
となります。これは便利です。覚えておけばどのような2次関数の頂点も求めることができます。
ただし、この公式を使っても、上記の



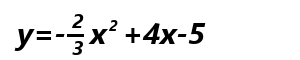
の頂点を求めるにはちょっと面倒な計算が必要になります。というわけで、最終兵器登場です！

微分

2次関数の頂点と接する接線の傾きは、常に０です。このことを利用して頂点を求めることができれば、計算がうんと楽になります。
というのも、傾きを求めるために微分するので、次数を一つ減らすことができ、定数項消えるので、共通因数の計算すらする必要がありません。完全マスター微分法
微分とは、ある関数の接線の傾きを求めることですから、導関数=0となるxが頂点のx座標です。
本当でしょうか？確かめてみましょう。関数、


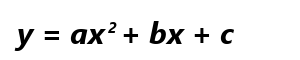
の頂点を微分を使って求めます。



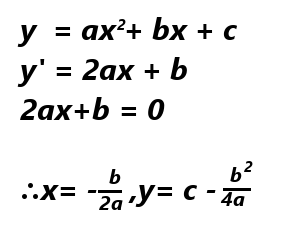
頂点が、平方完成を使って求めた、



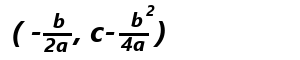
と等しいため、この方法は正しいといえます。
しかも、平方完成に比べ、微分を使えば同じ結果なのに計算が簡単になっていることがわかるとおもいます。
では、関数、



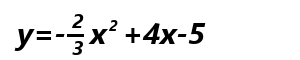
をこの方法で解いてみましょう。



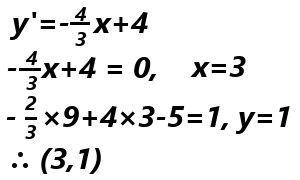
いとも簡単に解くことができました。

最後に今更ですが、この方法の手順をまとめます。

①導関数を求めます。

②導関数＝０となるxを求めます。

③与えられた関数に②で求めたxを代入してyを求めます。

結論

見ただけで平方完成で解けそうな簡単な式は平方完成で解くべし！

平方完成で解くのが面倒な式は微分を使うべし！

---

関連記事

完全マスター微分法
簡単に２次関数の頂点が求めれる微分法。ほかにも曲線の傾きや物体の瞬間の速度、加速度を求めるにに不可欠です。
ここでは超初心者にもわかりやすく解説しています。ぜひご一読ください。

---